机器学习:笔记 - Machine Learning Note
2. 模型评估与选择
2.1 经验误差与过拟合
在m个样本中有a个样本分类错误
- 错误率(Error rate): \(E = \frac{a}{m}\)
在训练集上的误差称
训练误差(training error)或经验误差(empirical error)
在新样本上的误差称泛化误差(generalization error) 精度(Accuracy): \(1 - E\)
过拟合(Overfitting): 模型在训练数据上表现很好,但在测试数据上表现糟糕,这通常是因为模型过于复杂,以至于“记住”了训练数据的噪声.
- 过拟合(Overfitting): 模型在训练数据上表现很好,但在测试数据上表现糟糕,这通常是因为模型过于复杂,以至于“记住”了训练数据的噪声.
与NP的关系:
若可以彻底避免过拟合,则通过经验误差最小化就可以获最优解,这就意味着我们构造性的证明了P = NP
2.2 评估方法
2.2.1 留出法
留出法(Hold-out Method) 留出法通常将数据集分为训练集(S)和测试集(T),有时还可以进一步将训练集分为训练集和验证集。在使用留出法时, 一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果
注意:
- 训练/测试集的划分要尽可能
保持数据分布的一致性, 避免因数据划分过程引入额外的偏差而对最终结果产生影响, 例如在分类任务中至少要保持样本的类别比例相似- 若令训练集S包含绝大多数样本, 则训练出的模型可能更接近于用D训练出的模型, 但由于T比较小,评估结果可能不够稳定准确; 若令测试集T多包含一些样本, 则训练集S与D差别更大了, 被评估的模型与用D训练出的模型相比可较大差别, 从而降低了评估结果的保真(fidelity)
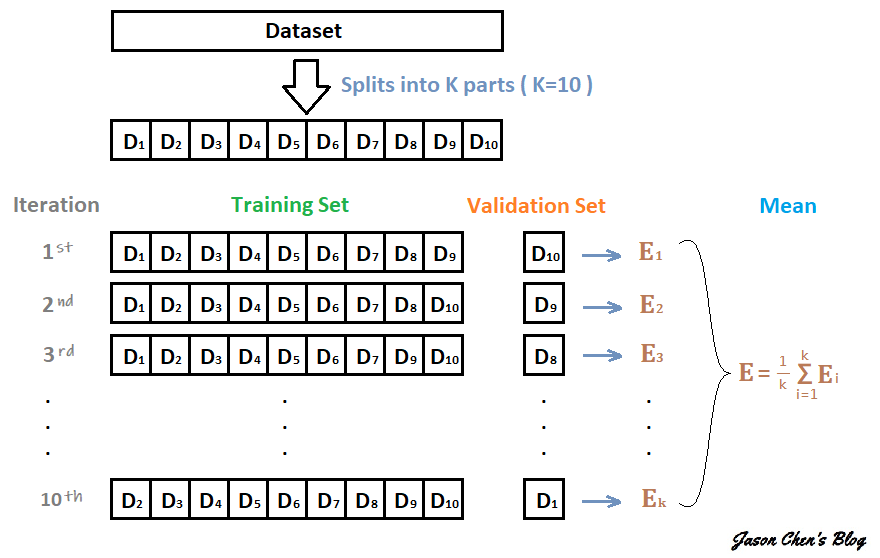
2.2.2 交叉验证法
交叉验证法(cross validation/k-fold cross validation)先将数据集D划分为k个大小相似的互斥自己.
- 每个子集\(D_i\)都尽可能保持数据分布的一致性, 即从D中通过分层采样得到.
- 每次用k-1个子集的并集作为训练集, 余下的那个子集作为测试集
- 这样就可获得k组训练/测试集, 从而可进行k次训练和测试, 最终返回的是这k个测试结果的均值.
缺点: 测试样本数量大时计算开销极大
k最常用取值是10, 此时成为”10折交叉验证”
数据集D划分为k个子集同样存在多种划分方式, 为减小因样本划分不同而引入的差别, k折交叉验证通常要随机使用不同的划分重复p次, 最终的评估结果是这p次k折交叉验证结果的均值, 例如常见的有”10次10折交叉验证”
2.2.3 自助法
自助法(bootstrapping)在给定包含m个样本的数据集, 对其采样产生数据集D’:
- 每次随即从D中挑选一个样本, 将其拷贝放入D
- 再将该样本放回初始数据集D中,使其仍有机会被再次采样
- 重复m次后,会获得包含m个样本的数据集D’
样本适中不被采到的概率为\((1-\frac{1}{m})^m\), 取极限为 0.368
- 约有36.8%样本未出现在采样数据集D’中, 这时用D’作为训练集, D\D’用作测试集
这样的测试结果成为”包外估计”(out-of-bag estimate)
优点: 在数据集较小时, 难以有效的划分训练/测试集时很有用; 能从初始数据集中产生多个不同的训练集, 对集成学习有好处
缺点: 改变了初始数据集的分布, 可能引入估计偏差
2.2.4 调参和最终模型
在进行模型估计和选择时, 除了要对使用学习算法进行选择, 还需对算法参数进行设定, 这就是通常所说的”参数调节”/”调参”(parameter tuning)
2.3 性能度量
对学习器的泛化性能进行评估, 不仅需要有效可行的实验估计方法, 还需要有衡量模型泛化能力的评价标准,即性能度量(performance measure)
在预测任务中, 给定样例集\(D = \{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}\), 其中\(y_i\)是实例\(x_i\)的真实标记. 要估计学习器\(f\)的性能, 就要把学习器预测结果\(f(x)\)与真实标记\(y\)进行比较
均方误差(mean squared error):
\[E(f;D) = \frac{1}{m}\sum\limits^m_{i=1}(f(x_i) - y_i)^2\]对于数据分布$D$和概率密度函数$p(·)$,均方误差可描述为:
\[E(f;D) = \int_{x\thicksim D}(f(x)-y)^2p(x)dx\]
2.3.1 错误率与精度
错误率定义为:
\[E(f;D) = \frac{1}{m}\sum\limits^m_{i=1}I(f(x_i)\neq y_i)\]精度定义为:
\[acc(f;D) = \frac{1}{m}\sum\limits^m_{i=1}I(f(x_i) = y_i) = 1 - E(f;D)\]更一般的,对于数据分布$D$和概率密度函数$p(·)$, 错误率和精度可分别表示为:
\[E(f;D) = \int_{x\thicksim D}I(f(x_i)\neq y_i)p(x) dx\] \[acc(f;D) = \int_{x\thicksim D}I(f(x_i) = y_i)p(x) dx = 1 - E(f;D)\]
2.3.2 查准率、查全率与F1
| 真实情况 | 预测结果: 正例 | 预测结果: 反例 |
|---|---|---|
| 正例 | TP | FN |
| 反例 | FP | TN |
查准率(precision):
\[P = \frac{TP}{TP+FP}\]查全率(recall):
\[R = \frac{TP}{TP + FN}\]平衡点(Break-Even Point)是”查准率=查全率”时的取值。更常用的是F1度量:
\[F1 = \frac{2 \times P \times R}{P + R} = \frac{2 \times TP}{样例总数 + TP - TN}\]\(F_\beta\)能够表达对查准率/查全率的不同的偏好, 定义为:
\[F_\beta = \frac{(1 + \beta^2) \times P \times R}{(\beta^2 \times P) + R}\]\(\beta > 1\)时查全率有更大影响, \(\beta < 1\)时查准率有更大影响
多次训练:
现在个混淆矩阵上分别计算出查准率和查全率, 记为\((P_1, R_1), (P_2, R_2),...,(P_n,R_n)\), 再计算平均值, 这样就得到”宏查准率”(macro-P)、”宏查全率”(macro-R), 以及相应的”宏F1”(macro-F1):
也可先将各混淆矩阵的对应元素进行平均, 得到\(TP、FP、TN、FN\)的平均值,分别记得\(\overline{TP}、\overline{FP}、\overline{TN}、\overline{FN}\), 再基于这些平均值算出”微查准率”(micro-P)、”微查全率”(micro-R)和”微F1”(micro-F1):
\[micro-P = \frac{\overline{TP}}{\overline{TP}+\overline{FP}}\] \[micro-R = \frac{\overline{TP}}{\overline{TP}+\overline{FN}}\] \[micro-F1 = \frac{2 \times micro-P \times micro-R}{micro-P + micro-R}\]
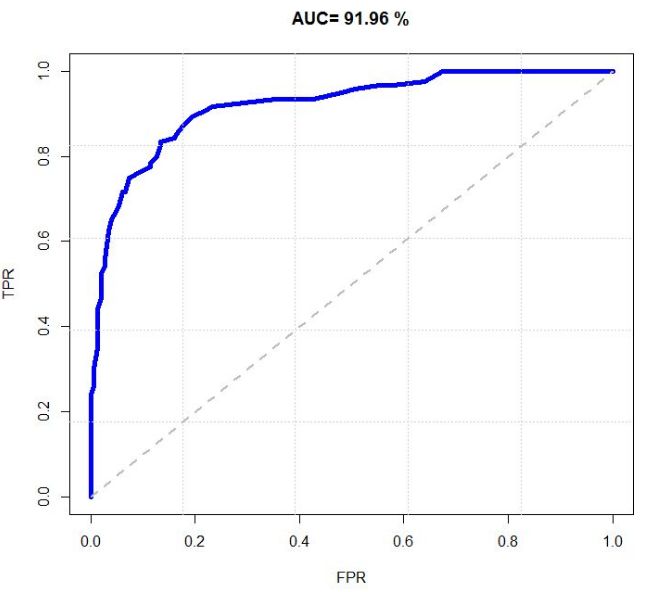
2.3.3 ROC与AUC
ROC全称”受试者工作特征”(Receiver Operating Characteristic)曲线。ROC曲线的纵轴时”真正例率”(True Positive Rate, 简称TPR), 横轴是”假正例率”(Flase Positive Rate, 简称FPR), 定义为:
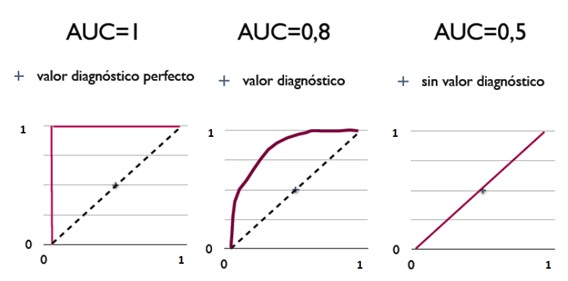
\[TPR = \frac{TP}{TP + FN}\] \[FPR = \frac{FP}{TN + FP}\]与P-R图类似,若一个学习器的ROC曲线被另一个学习器的曲线完全包裹, 则可以断言后者的性能优于前者.若两个学习器的ROC曲线发生交叉, 则难以一般性地断言两者孰优孰劣. 此时应比较ROC曲线下的面积, 即AUC(Area Under ROC Curve), 可估算为
\[AUC = \frac{1}{2}\sum\limits^{m-1}_{i=1}(x_{i+1}-x_i)·(y_i+y_{i+1})\]AUC考虑的时样本预测的排序质量, 因此它与排序误差有紧密联系. 给定\(m^+\)个正例和\(m^-\)个反例, 令\(D^+\)和\(D^-\)分别表示正反例集合, 则排序损失(loss)定义为:
\[l_{rank} = \frac{1}{m^+m^-}\sum\limits_{x^+\in D^+}\sum\limits_{x^-\in D^-}(I(f(x^+)<f(x^-))+\frac{1}{2}I(f(x^+)=f(x^-)))\] \[AUC = 1 - l_{rank}\]
2.3.4 代价敏感错误率与代价曲线
为权衡不同类型错误所造成的不同损失, 可谓错误赋予”非均等代价”(unequal cost)
| 真实类别 | 预测类别: 第0类 | 预测类别: 第1类 |
|---|---|---|
| 第0类 | 0 | $cost_{01}$ |
| 第1类 | $cost_{10}$ | 0 |
在非均等代价下,我们所希望的不再是简单的最小化错误次数, 而是希望最小化”总体代价”(total cost). “代价敏感”(cost-sensitive)错误率为:
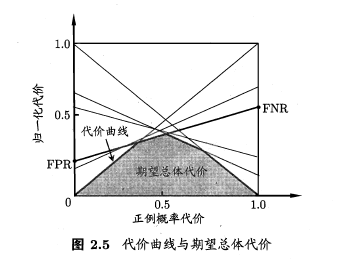
\[E(f;D;cost)=\frac{1}{m}(\sum\limits_{x_i\in D^+}I(f(x_i)\neq y_i) \times cost_{01}+ \sum\limits_{x_i\in D^-}I(f(x_i)\neq y_i) \times cost_{10})\]在非均等代价下, ROC曲线不能直接反映出学习器的期望总体代价, 而”代价曲线”(cost curve)则可达到该目的. 代价曲线图的横轴时取值为[0,1]的正例概率代价:
\[P(+)cost = \frac{p \times cost_{01}}{p \times cost_{01} + (1 - p)\times cost_{10}}\]其中\(p\)是样例为正例的的概率, 纵轴是取值为[0,1]的归一化代价
\[cost_{norm} = \frac{FNR \times p \times cost_{01}+ FPR \times (1-p)\times cost_{10}}{p \times cost_{01} + (1-p)\times cost_{10}}\]2.4 比较检验
2.4.1 假设验证(hypothesis test)
在包含m个样本的测试集上, 泛化错误率为\(\epsilon\)的学习器被测得测试错误率为\(\hat{\epsilon}\)的概率:
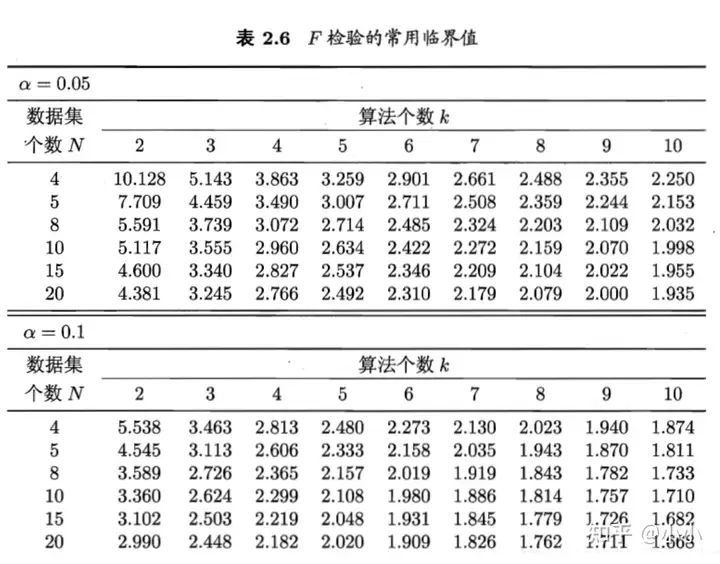
\[P(\hat{\epsilon};\epsilon) = \begin{pmatrix} m \\ \hat{\epsilon} \times m \end{pmatrix} \epsilon^{\hat{\epsilon} \times m}(1 - \epsilon)^{m - \hat{\epsilon} \times m}\]\(\alpha\)的常用取值有0.05, 0.1
这里\(1-\alpha\)反映了结论的”置信度”(confidence),直观来看, 即非阴影部分的面积
\[\bar{\epsilon} = min \epsilon \space s.t. \space \sum\limits^m_{i = \epsilon \times m + 1} \begin{pmatrix} m \\ i \end{pmatrix}\epsilon^i_0(1 - \epsilon_0)^{m-i} < \alpha\]通过多次重复留出法或是交叉验证法等进行多次训练/测试, 这样会得到多个测试错误率, 此时可使用”t检验”(t-test). 假定我们得到了一个k个测试错误率, \(\hat{\epsilon}_1, \hat{\epsilon}_2, ..., \hat{\epsilon}_k\), 则平均测试错误率\(\mu\)和方差\(\sigma^2\)为
\[\mu = \frac{1}{k}\sum\limits^k_{i=1}\hat{\epsilon}_i\] \[\sigma^2 = \frac{1}{k - 1}\sum\limits^k_{i=1}(\hat{\epsilon}_i-\mu)^2\]考虑到这k个测试错误率可看作泛化错误率\(\epsilon_0\)的独立采样, 则变量
\[\tau_t = \frac{\sqrt{k}(\mu - \epsilon_0)}{\sigma}\]| \(\alpha\) | k = 2 | k = 5 | k = 10 | k = 20 | k = 30 |
|---|---|---|---|---|---|
| 0.05 | 12.706 | 2.776 | 2.262 | 2.093 | 2.045 |
| 0.10 | 6.314 | 2.132 | 1.833 | 1.729 | 1.699 |
2.4.2 交叉验证t检验
对两个学习器A和B, 若我们使用k折交叉验证法得到的测试错误率分别为\(\epsilon^A_1, \epsilon^A_2, ..., \epsilon^A_k\)和\(\epsilon^B_1, \epsilon^B_2, ..., \epsilon^B_k\), 其中\(\epsilon^A_i\)和\(\epsilon^B_i\)是在相同的第i折训练/测试集上得到的结果, 则可用k折交叉验证”成对t检验”(paired t-tests)来进行比较检验
这里的基本思想是若两个学习器的性能相同, 则它们使用相同的训练/测试集得到的测试错误率应相同, 即\(\epsilon^A_i = \epsilon^B_i\)
具体来说, 对k折交叉验证产生的k对测试错误率:
- 先对每对结果球差, \(\Delta_i = \epsilon^A_i - \epsilon^B_i\)
- 若两个学习器性能相同, 则差值均值应为0.
因此, 可根据差值, 来对学习器A与B性能相同这个假设做t检验, 计算出差值的均值\(\mu\)和方差\(\sigma^2\), 在显著度\(\alpha\)下,若变量
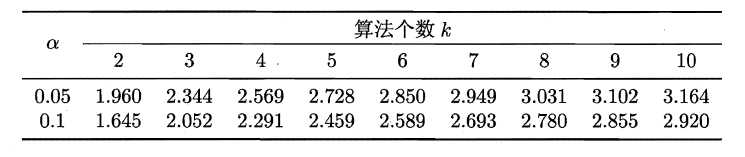
\[\tau_t = \vert\frac{\sqrt{k}\mu}{\sigma}\vert\]小于临界值\(t_{\alpha/2, k-1}\), 则假设不能被拒绝, 即认为两个学习器的性能没有显著差别
- 否则可认为两个学习器的性能有显著差别, 且平均错误率较小的那个学习器性能较优
因为样本有限, 在使用交叉验证等实验估计法时, 不同轮次的训练集会有一定的重叠, 为缓解这个问题可以使用”5x2交叉验证”
2.4.3 McNemar检验
对于二分问题, 使用留出法不仅可估计出学习器A和B的测试错误率, 还可获得两学习器分类结果的差别, 即两者都正确、都错误、一个正确一个错误的样本数:
| 算法B | 算法A: 正确 | 算法A: 错误 |
|---|---|---|
| 正确 | \(e_{00}\) | \(e_{01}\) |
| 错误 | \(e_{10}\) | \(e_{11}\) |
| 若我们做的假设是两学习器性能相同, 则应有\(e_{01} = e_{10}\), 那么变量$$ | e_{01} - e_{10} | $$应当服从正态分布. McNemar检验考虑变量 |
服从自由度为1的\(X^2\)分布, 即标准正态分布变量的平方.
- 当以上变量值小于临界值\(X^2_\alpha\)时, 不能拒绝假设, 即认为两学习器的性能没有显著差别
- 否则拒绝假设, 即认为两学习器性能有显著差别, 且平均错误率较小的那个学习器性能较优
2.4.4 Friedman检验与Nemenyi后续检验
| 数据集 | 算法A | 算法B | 算法C |
|---|---|---|---|
| \(D_1\) | 1 | 2 | 3 |
| \(D_2\) | 1 | 2.5 | 2.5 |
| \(D_3\) | 1 | 2 | 3 |
| \(D_4\) | 1 | 2 | 3 |
| 平均序值 | 1 | 2.125 | 2.875 |
使用Friedman检验来判断这些算法是否性能相同.若相同, 则他们的平均序列应当相同.假定我们在N个数据集上比较k个算法, 令\(r_i\)表示第i个算法的平均序值, (不考虑平分序值)则\(r_i\)的均值和方差分别为\((k+1)/2\)和\((k^2-1)/12N\). 变量
\[\tau_{X^2} = \frac{k -1}{k}·\frac{12N}{k^2 - 1} \sum\limits^k_{i = 1}(r_i - \frac{k + 1}{2})^2\] \[=\frac{12N}{k(k+1)}(\sum\limits^k_{i=1}r_i^2-\frac{k(k+1)^2}{4})\]在k和N都较大时, 服从自由度为k-1的\(X^2\)分布
然而上述的圆石Friedman检验过于保守, 现在通常使用变量
\[\tau_F = \frac{(N - 1)\tau_{X^2}}{N(k - 1) - \tau_{X^2}}\]若”所有算法的性能相同”这个假设被拒绝, 则说明算法的性能显著不同.这时需进行”后续检验”(post-hoc test)来进一步区分个算法. 常用的有Nemenyi后续检验.
Nemenyi检验计算出平均序值差别的临界值域
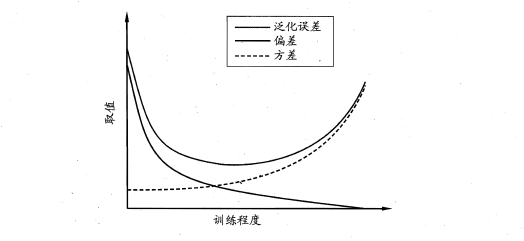
\[CD = q_\alpha\sqrt{\frac{k(k+1)}{6N}}\]2.5 偏方与方差
在回归任务中
学习算法的期望预测:
\[\bar{f}(x) = E_D[f(x;D)]\]使用样本数相同的不同训练集产生的方差为:
\[var(x) = E_D[(f(x;D)-\bar{f}(x))^2]\]噪声为:
\[\varepsilon^2 = E_D[(y_D - y)^2]\]期望输出与真是标记的差别成为偏差(bias), 即:
\[bias^2(x) = (\bar{f}(x)-y)^2\]泛化误差可分解为偏差、方差、与噪声之和
\[E(f;D) = bias^2(x) + var(x) + \varepsilon^2\]3. 线性模型
3.1 基本形式
给定有d个属性描述的实例\(\vec{x} = (x_1;x_2;...;x_d)\), 其中\(x_i\)是x在第i个属性上的取值, 线性模型(linear model)试图学得一个通过属性的线性组合来进行预测的函数, 即
\[f(\vec{x}) = w_1x_1 + w_2x_2 + ... + w_dx_d + b,\]一般用向量形式写成
\[f(\vec{x}) = \vec{w}^T\vec{x} + b\]3.2 线性回归
给定数据集\(D = {(x_1, y_1), (x_2, y_2),...,(x_m,y_m)}\), 其中\(x_i = (x_{i1};x_{i2};...;x_{id}), y_i \in R\)
线性回归试图学得
\[f(x_i) = wx_i + b, 使得f(x_i)\simeq y_i\]均方误差最小化:
\[(w^*, b^*) = \arg min\sum\limits^m_{i=1}(f(x_i) - y_i)^2\] \[= \arg min \sum\limits^m_{i=1}(y_i - wx_i - b)^2\]\(w^*, b^*\)表示\(w\)和\(b\)的解
均方误差有非常好的几何意义, 它对应了常用的欧几里得距离或简称”欧式距离”(Euclidean distance). 基于均方误差最小化来进行模型求解的方法成为”最小二乘法“(least square method).
求解\(w\)和\(b\)使\(E_{(w,b)} = \sum^m_{i=1}(y_i - wx_i- b)^2\)最小化的过程, 称为线性回归模型的最小二乘”参数估计”(parameter estimation). 我们可将\(E_{(w,b)}\)分别对\(w\)和\(b\)求导, 得到
\[\frac{\partial E_{w,b}}{\partial E_w} = 2 (w\sum\limits^m_{i=1}x_i^2 - \sum\limits^m_{i = 1}(y_i - b)x_i)\] \[\frac{\partial E_{w,b}}{\partial E_w} = 2 (mb - \sum\limits^m_{i = 1}(y_i - wx_i))\]然后令上两式为0, 可得到$w$和$b$最优解的闭式(closed-form)解
\[w = \frac{\sum\limits^m_{i=1}y_i(x_i - \bar{x})}{\sum\limits^m_{i = 1}x^2_i - \frac{1}{m}(\sum\limits^m_{i = 1}x_i)^2}\] \[b = \frac{1}{m}\sum\limits^m_{i = 1}(y_i - wx_i)\]其中\(\bar{x} = \frac{1}{m}\sum\limits^m_{i = 1}x_i\)为\(x\)的均值
更一般的形式为:
\[f(\vec{x}_i) = \vec{w}_T\vec{x}_i + b, 使得f(\vec{x}_i)\simeq y_i\]这称为”多元线性回归“(multivariate linear regression)
可利用最小二乘法来对\(\vec{w}\)和\(b\)进行估计. 为便于讨论, 我们把\(\vec{w}\)和\(b\)吸收入向量形式\(\hat{\vec{w}}=(\vec{w};b)\), 相应的, 把数据集D表示为一个\(m\times(d+1)\)大小的矩阵\(\vec{X}\),其中每行对应于一个示例, 该行前\(d\)个元素及对应于实例的\(d\)个属性值, 最后一个元素恒置为1, 即
\[\vec{X} = \begin{pmatrix} x_{11} & x_{12} & ... & x_{1d} & 1 \\ x_{21} & x_{22} & ... & x_{2d} & 1 \\ ... & ... & ... & ... & ... \\ x_{m1} & x_{m2} & ... & x_{md} & 1 \end{pmatrix} = \begin{pmatrix} \vec{x}^T_1 & 1 \\ \vec{x}^T_2 & 1 \\ ... & ... \\ \vec{x}^T_m & 1 \end{pmatrix}\]再把标记也写成向量形式\(\vec{y} = (y_1;y_2;...;y_m)\), 有
\[\hat{\vec{w}}^* = \arg\limits_{\hat{\vec{w}}}\min(\vec{y} -\vec{X}\hat{\vec{w}})^T(\vec{y} - \vec{X}\hat{\vec{w}})\]令\(E_{\hat{\vec{w}}} = (\vec{y} -\vec{X}\hat{\vec{w}})^T(\vec{y} - \vec{X}\hat{\vec{w}})\), 对\(\hat{\vec{w}}\)求导得到
\[\frac{\partial E_{\hat{\vec{w}}}}{\partial\hat{\vec{w}}} = 2 \vec{X}^T(\vec{X}\hat{\vec{w}} - \vec{y})\]当\(X^TX\)为满秩矩阵(full-rank matrix)或正定矩阵(positive definite matrix)时, 上式为零可得
\[\hat{\vec{w}}^* = (\vec{X}^T\vec{X})^{-1}\vec{X}^T\vec{y}\]其中\((\vec{X}^T\vec{X})^{-1}\)是矩阵\((\vec{X}^T\vec{X})\)的逆矩阵. 令\(\hat{\vec{x}}_i = (\vec{x}_i,1)\),则最终学得的多元线性回归模型为
\[f(\hat{x}_i) = \hat{x}^T_i(X^TX)^{-1}X^Ty\]假设我们认为示例所对应的输出标记是在指数尺度上变化, 那就可将输出标记的对数作为线性模型逼近的目标, 即
\[\ln y = \vec{w}^T\vec{x} + b\]这就是”对数线性回归”(log-linear regression), 它实际上是在试图让\(e^{\vec{w}^T\vec{x}+b}\)逼近\(y\).
其作用是把一个非线性关系通过对数形式转换成线性关系
更一般的,考虑单调可微函数\(g(·)\), 令
\[y = g^{-1}(\vec{w}^T\vec{x}+b)\]这样得到的模型成为”
广义线性模型“(generalized linear model),其中函数\(g(·)\)称为”联系函数“(link function).通过联系函数把非线性关系转换成线性关系,\(\ln(·)\)就是其中一种
3.3 对数几率回归(逻辑回归)
线性回归产生的预测值:
对数几率函数(logistic function):
对数几率函数(逻辑回归函数)通过函数把需要分类的值(这里指二元分类)压缩成一个连续的阶跃函数
几率(odds):
对数几率(logit):
通过以上式子可得:
\[p(y = 1|x) = \frac{e^{\vec{w}^T\vec{x}+b}}{1+e^{\vec{w}^T\vec{x}+b}} \\ p(y = 0|x) = \frac{1}{1+e^{\vec{w}^T\vec{x}+b}}\]可通过”极大似然法“(maximum likelihood method)来估计\(w\)和\(b\). 给定数据集\(\{(\vec{x}_i,y_i)\}^m_{i = 1}\), 对率回归模型最大化”对数似然”(log-likelihood)
即令每个样本属于其真实标记的概率越大越好.
为便于讨论
令\(\beta = (\vec{w};b)\), \(\hat{\vec{x}} = (\vec{x};1)\)
即 \(p(y_i|\vec{x}_i;\vec{w}, b) = y_ip_1(\hat{\vec{x}}_i; \beta) + (1 - y_i) p_0 (\hat{\vec{x}}_i; \beta)\)
结合上式,并最大化可获得: \(\ell(\beta) = \sum^m_{i=1}(-y_i\beta^T\hat{\vec{x}}_i+ \ln(1+e^{\beta^T\hat{\vec{x}}_i}))\)
根据凸优化理论,利用优化算法可得: \(\beta^* = \argmin\limits_\beta l(\beta)\) 以牛顿法为例: \(\beta' = \beta - (\frac{\partial^2\ell(\beta)}{\partial\beta\partial\beta^T})^{-1}\frac{\partial \ell(\beta)}{\partial\beta}\\ \frac{\partial\ell(\beta)}{\partial\beta} = - \sum^m_{i = 1} \hat{\vec{x}_i}(y_i - p_1(\hat{\vec{x}_i; \beta}))\\ \frac{\partial^2\ell(\beta)}{\partial\beta\partial\beta^T} = \sum^m_{i=1}\hat{\vec{x}}_i\hat{\vec{x}}_i^Tp_1(\hat{\vec{x}}_i; \beta)(1 - p_1(\hat{\vec{x}}_i; \beta))\)
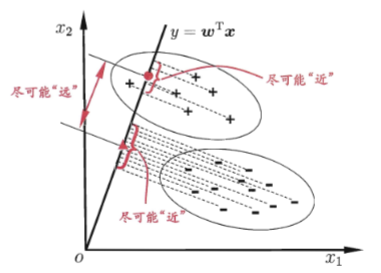
3.4 线性判别分析
欲使同样样例的投影点尽可能接近,可以让同类样例投影点的协方差尽可能小,即 \(\vec{w}^T\sum_0\vec{w} + \vec{w}^T\sum_1\vec{w}\)尽可能小
欲使异类样例的投影点尽可能远离,可以让类中心之间的距离尽可能大,即 \(||\vec{w}^T\mu_0 - \vec{w}^T\mu_1||^2_2\)尽可能小
\[\begin{aligned}\text{J}&=\frac{\|\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_0-\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_1\|_2^2}{\boldsymbol{w}^\mathrm{T}\boldsymbol{\Sigma}_0\boldsymbol{w}+\boldsymbol{w}^\mathrm{T}\boldsymbol{\Sigma}_1\boldsymbol{w}}\\&=\frac{\boldsymbol{w}^\mathrm{T}(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^\mathrm{T}\boldsymbol{w}}{\boldsymbol{w}^\mathrm{T}(\boldsymbol{\Sigma}_0+\boldsymbol{\Sigma}_1)\boldsymbol{w}} .\end{aligned}\]定义“类内散度矩阵”(within-class scatter matrix) \(\begin{aligned} \mathbf{s}_{w}& =\boldsymbol{\Sigma}_0+\boldsymbol{\Sigma}_1 \\ &=\sum_{x\in X_{0}}\left(\boldsymbol{x}-\boldsymbol{\mu}_{0}\right)\left(\boldsymbol{x}-\boldsymbol{\mu}_{0}\right)^{\mathrm{T}}+\sum_{x\in X_{1}}\left(\boldsymbol{x}-\boldsymbol{\mu}_{1}\right)\left(\boldsymbol{x}-\boldsymbol{\mu}_{1}\right)^{\mathrm{T}} \end{aligned}\)
参考书籍: 《机器学习》- 周志华著